The adaptive logic programme aims at developing a type of formal logics (and the connected metatheory) that is especially suited to explicate the many interesting dynamic consequence relations that occur in human reasoning but for which there is no positive test (see the next section). Such consequence relations occur, for example, in inductive reasoning, handling inconsistent data, …
The explication of such consequence relations is realized by the dynamic proof theories of adaptive logics. These proof theories are dynamic in that formulas derived at some stage may not be derived at a later stage, and vice versa.
The programme is application driven. This is one of the reasons why the predicative level is considered extremely important, even if, for many adaptive logics, the basic features of the dynamics are already present at the propositional level. The main applications are taken from the philosophy of science; some also from more pedestrian contexts.
Much interesting actual reasoning displays two forms of non-standard dynamics.
- An external dynamics: a conclusion may be withdrawn in view of new information. This means that the consequence relation is non-monotonic.
- An internal dynamics: a conclusion may be withdrawn in view of the better understanding of the premises provided by a continuation of the reasoning.
While examples of logics displaying the external dynamics are available, logicians did not pay much attention to the internal dynamics. And yet it is very familiar to anyone. Reasoning from one’s convictions, one often derives a consequence that one later rejects, even if one’s convictions were not modified. The point is that humans are unable to see at once all the consequences of a set of premises (in this case, one’s convictions).
To clearly understand the two forms of dynamics, it is useful to compare them to the standard forms of logical dynamics. These are common to all reasoning, and well known from usual logics. First consider the standard external dynamics. If we are reasoning (by some logic L) from a set of data  and, at some point in time, are supplied with a supplementary set of data
and, at some point in time, are supplied with a supplementary set of data  ‘, we are in general able to derive more consequences from that point in time on. Formally: CnL(
‘, we are in general able to derive more consequences from that point in time on. Formally: CnL( )
) 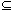 CnL(
CnL(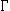
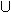
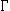 ’). Next consider the standard internal dynamics. Given a set of rules of inference, not all formulas derivable from a set of premises are derivable by a single application of a rule at some stage of a proof. The set of formulas derivable by a single application of a rule monotonically increases as the proof proceeds. A different form of dynamics is related to the fact that humans are unable to see at once all the consequences of a set of premises. As a result, some statements will only be seen to be derivable from the premises after other statements have been derived. The derivability of a statement, however, does not depend on the question whether one sees that it is derivable. So, this form of internal dynamics is related to logical heuristics and to computational aspects, rather than of the logic properly. To be more precise: the formulation of the proof theory is fully independent of it. As we shall see later, the matter is completely different for consequence relations that display an adaptive internal dynamics.
’). Next consider the standard internal dynamics. Given a set of rules of inference, not all formulas derivable from a set of premises are derivable by a single application of a rule at some stage of a proof. The set of formulas derivable by a single application of a rule monotonically increases as the proof proceeds. A different form of dynamics is related to the fact that humans are unable to see at once all the consequences of a set of premises. As a result, some statements will only be seen to be derivable from the premises after other statements have been derived. The derivability of a statement, however, does not depend on the question whether one sees that it is derivable. So, this form of internal dynamics is related to logical heuristics and to computational aspects, rather than of the logic properly. To be more precise: the formulation of the proof theory is fully independent of it. As we shall see later, the matter is completely different for consequence relations that display an adaptive internal dynamics.
Many consequence relations are undecidable and the predicative versions of nearly all logics are undecidable. If a logic is undecidable but monotonic, there still may be a positive test for derivability. However, if a consequence relation is undecidable and non-monotonic, there can only be a positive test for it in some rather artificial cases. There may at best be a definition of consequence relation in terms of a monotonic logic or in terms of a semantics or in terms of continuations of a proof. And as a logic may be decidable for certain fragments of the language, there may also be criteria for derivability.
A general characteristic of the consequence relations mentioned in the previous section is that certain inferences are considered as correct iff certain formulas behave normally. What normality means will depend on the adaptive logic. In an inconsistency-adaptive logic, abnormalities are inconsistencies (possibly of a specific form); in some adaptive logics of induction, abnormalities are negations of generalizations (for example: ~(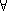 x)(Px
x)(Px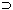 Qx)). In some (prioritized) adaptive logics, abnormalities (of some priority level) are negations of premises (of that priority) — see the section on Flat and prioritized adaptive logics for an example.
Qx)). In some (prioritized) adaptive logics, abnormalities (of some priority level) are negations of premises (of that priority) — see the section on Flat and prioritized adaptive logics for an example.
An adaptive logic supposes that all formulas behave normally unless and until proven otherwise. Moreover, if an abnormality occurs, it is considered as local. This means that, even if some formula behaves abnormally, all other formulas are still supposed to behave normally unless and until proven otherwise. We shall see the effect of this in the following section.
While some consequences of a set of premises depend on the normal behaviour of certain formulas, other consequences follow come what may. Thus, an adaptive logic of induction enables one to derive certain generalizations as well as certain ‘predictions’ from a set of premises. To do so, one relies on the supposition that formulas behave normally unless and until proven otherwise. However, the premises also have deductive consequences that follow independently of any normality suppositions.
This naturally leads to seeing an adaptive logic as defined by three elements: the lower limit logic, a set of abnormalities, and an adaptive strategy.
· The lower limit logic determines which consequences hold independently of any presuppositions (or conditions).
· A set of abnormalities, which is characterized by a logical form. For example, the set of abnormalities may contain the existential closure of all formulas of the form A&~A. This logical form may be restricted. For example, the formulas of the form A&~A may be restricted to those in which A is a primitive formula (a schematic letter for sentences, a primitive predicative formula, or an identity). Extending the lower limit logic with an axiom that rules out the occurrence of abnormalities, results in the upper limit logic. In other words, the set of lower limit models that verify no abnormality are the upper limit models. The upper limit logic determines which consequences follow in the normal situation.
· An adaptive strategy. If an abnormality is derivable from the premises (by the lower limit logic), the upper limit logic reduces the premises (or theory) to triviality. However, the adaptive logic still interprets the premises “as normally as possible”. This phrase is ambiguous: there are several ways to do so. The adaptive strategy will pick one specific way to interpret the premises as normally as possible.
This clarifies the way in which adaptive logics adapt themselves to specific premises. The logic interprets the premises in agreement with the lower limit logic and, moreover, as much as possible in agreement with the upper limit logic. If some formulas (premises or lower limit consequences of the premises) are abnormal, the adaptive logic will not add the upper limit consequences of these formulas.
(Universiteit Gent, Centre for Logic and Philosophy of Science)
http://logica.ugent.be/adlog/al.html
 and, at some point in time, are supplied with a supplementary set of data
and, at some point in time, are supplied with a supplementary set of data 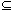 CnL(
CnL(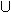
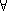 x)(Px
x)(Px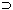 Qx)).
Qx)).